Why Are Galaxies Disks?
Not all galaxies are disks, but many are. The reasons have to do with their formation history and a few basic physical laws.
The short answer as to why disk galaxies have the shape they have is angular momentum. That phrase by itself is not very illuminating. Even if you know what angular momentum is, you still might not understand why it causes some galaxies to take on the shape of a disk, while others do not. The important difference between the two types of galaxies is the history of their formation, but before we get to that we will look at how disk galaxies form.
Galaxies started to form early in the history of the universe. They formed as the result of the collapse of enormous clouds of gas, mostly hydrogen and helium. These were attracted by the gravity of dark matter concentrations that had emerged from the initial density field of the Big Bang. As these clouds collapsed, material that had originally been distributed quite widely began to concentrate into relatively small volumes. Many collisions occurred between different parcels within the collapsing gas clouds, and these collisions set the galaxies onto the path of become disk galaxies like spirals.
The Law of Conservation of Momentum
To understand why collisions in gas are important, you must realize that when gas clouds collide they dissipate enormous amounts of energy. During a collision the gas compresses and heats. The hot gas begins to emit radiation, as x-rays, visible light or infrared, depending on the violence of the collision. As a result, the energy of the collision, originally the kinetic energy of the bulk motion of the gas clouds, is radiated away. This is a consequence of the law of conservation of energy, which states that energy cannot be created or destroyed, only shifted around in form. To summarize, in the process of these collisions the gas initially heats up. It then radiates away vast amounts of energy and cools again, often below its pre-collision temperature.
What’s more, the motion of the gas is greatly altered, perhaps even arrested, as a result of the collision. Due to conservation of linear momentum, colliding gas clouds that are initially moving at great speeds before they collide can be brought to a near standstill afterward. We can make this less abstract by considering an specific example.
We could imagine two clouds of gas of the same mass that move toward each other with exactly the same speed. However, a more familiar analogy might serve us better at the outset. So to begin with, picture two locomotives moving toward each other along a single set of railroad tracks. When they collide, they will abruptly stop. A few locomotive parts will fly in all directions, while most of each locomotive will be crumpled and stopped at the point of the collision. Most of the initial energy of their motion is spent compressing the locomotives, but some of it is carried away by the flying parts and the loud crashing sounds emitted. Colliding clouds of gas in space do something quite similar.
The clouds stop, just as the colliding locomotives do. They also become greatly compressed and heat up as a result. A great deal of the kinetic energy that was stored in their motion through space, their kinetic energy, is converted into heat as they compress. This heat is then radiated away via electromagnetic radiation, i.e. visible light, x-rays, infrared etc. Eventually all the energy is radiated away, leaving the clouds cold and much denser than before the collision.
Now imagine that one of the clouds (or locomotives) is slightly heavier than the other, or perhaps it is moving slightly faster (or both). In that case, the collision will still happen in essentially the way it’s described above, but the clouds (or locomotives) will not be completely stopped afterward. They will be combined into a single mass moving along in the direction of the faster/heavier cloud - or locomotive. This is because the original momentum of the system, which is the sum of the momenta of each object, is conserved. Or put another way, the total momentum before the collision is the same as the total momentum after the collision.
We can put this onto a mathematical footing as follows. If we use the fact that momentum (usually denoted by p… Don’t ask me why, I don’t know) is the product of an object’s mass and velocity, then we define momentum as below.
$$\vec{p}=m\vec{v}$$
The small arrows on the p and the v indicate that they are vectors, objects that have both a size (or amount of) and a direction. We need to use a vector because moving 5 mph to the left, for example, is not the same as moving 5 mph to the right, or forward or backward. The little arrows remind us about this fact. They tell us one other important thing as well. The momentum has a direction that is the same as the direction as the motion. This makes sense intuitively, but it is made mathematically clear because both sides of the equation are the same vector - that is what an equation means - and so both have the same direction.
Note that the mass \(m\) does not have an arrow. That is because mass is not a vector; it has no direction. Mass is what is called a scalar in the vernacular of physics. It is just a plain number (with units, of course, in this case kilograms). Do not confuse mass with weight. Weight is the force that gravity exerts, and force definitely has a direction, so it is a vector. If you want to get a better understanding of vectors, have a look at the blog post about vectors on this site.
The total momentum of the system comprised of the two clouds in the collision is the sum of their individual momenta. We can write that as follows.
$$\vec{P}=\vec{p}_1+\vec{p}_2$$
The upper case denotes to total momentum in the system, and the subscripts are labels used to refer to the individual clouds. We could have used \(\vec{p_a}\) or \(\vec{p_b}\) instead if we wanted to. We just need something to keep them straight in our mind. If the concept of vectors is not familiar to you, have a look at my vector tutorial to get the general idea of what they are and how they work. Many objects in physics are represented by vectors, so knowing even a little bit about them is immensely useful.
The equation above is generally true, but we can simplify things if we imagine that the two clouds move toward each other along a line in one dimension, call it the \(x\)-axis of some coordinate system. We do not lose any generality by doing this because we are free to choose any orientation we like for a set of coordinates that we use to describe this system. Since we are dealing with one-dimensional motion we can write the total momentum as below.
$$P = p_1 -p_2$$
We have here assumed that cloud 1 moves in the positive \(x\) direction (generally defined as to the right) and cloud 2 moves in the negative \(x\) direction (to the left under the usual conventions). Now we can substitute using the definition of momentum.
$$ MV = m_1 v_1 -m_2 v_2 $$
We again use upper case to denote the values after the collision. If we assume that the loss of mass in the collision is negligible, then we know that the total mass is the same before and after, and thus \(M = m_1 + m_2\). So we simplify further.
$$ (m_1+m_2)V = m_1 v_1 -m_2 v_2 $$
Now we can write the velocity of the system after the collision by dividing both sides by the total mass, \(m_1+m_2 \).
$$ V = \frac{m_1 v_1 -m_2 v_2}{m_1+m_2} $$
From this we can see that when the initial momentum (\(m_1v_1\)) of cloud 1 is larger than the momentum (\(m_2v_2\)) of cloud 2, then the final velocity of the merged cloud is positive, or in other words, it is in the initial direction of cloud 1. However, when the initial momentum of cloud 2 is larger, then the final velocity of the cloud is negative, in the initial direction of cloud 2. In the event that the two momenta are identical, the clouds stop dead, just as in the very first example we imagined. Take careful consideration that the final result does not depend on which of the clouds is initially moving faster, it depends upon which has the larger momentum initially. That momentum can consist of a small cloud moving relatively fast, or a larger cloud moving relatively slow. It is the product of the mass and velocity that tell us the momentum. In any case, the total momentum of the system is the same before and after the collision because it is conserved.
So what does all of this have to do with the shapes of galaxies? Just this. There will be numerous little cloudlets in a protogalactic cloud, and they will undergo collisions like that described above. In some cases the final velocity of a cloud-cloud collision will result in a “positive” final velocity. In others the final velocity will be “negative,” where positive and negative just means that the combined cloud that is formed by the collision can move in the initial direction of either of the two colliding cloudlets; each collision has its own specific \(x\)-axis orientation aligned along the direction from which the two clouds approach one another. The point is that after each collision the final combined cloud is moving along in the direction of one of the original clouds. The collisions will happen over and over again, forming larger cloudlets out of the original smaller ones. Eventually, everything will have settled down into one giant cloud of gas.
As an aside, on much smaller scales, some of these collisions can result in the formation of stars. That is another topic entirely, and much more detailed physics is involved.
So after everything is settled down and all the smaller cloudlets have merged into a single big cloud, the big cloud will likely be moving through space with a velocity determined by the resultant velocity of all the collisions that formed it. This is just the velocity corresponding to the total momentum of the system. In other words, it is the momentum we would get if we summed up all the cloud momenta from all the little cloudlets in the original protogalactic cloud before any collisions happened at all! So if we have \(n\) cloudlets in the protogalactic gas cloud, then the total momentum of the cloud can be written as the sum below, and its velocity through space can be found by dividing this momentum by the total mass of the cloud.
$$ \vec{P}=\vec{p}_1+\vec{p}_2+\vec{p}_3+\vec{p}_4+...+\vec{p}_{n-1}+\vec{p}_n $$
$$\vec{V}= \frac{\vec{p}_1+\vec{p}_2+\vec{p}_3+\vec{p}_4+...+\vec{p}_{n-1}+\vec{p}_n}{ m_1+m_2+m_3+m_4+…+m_{n-1}+m_n} $$
While the momentum of each individual cloudlet can be transferred to and shared with other cloudlets, the total momentum of the cloud as a whole, as described in the sum above, will remain constant. This is true no matter how many collisions and mergers of cloudlets happen. In particular, it is true after all the cloudlets have settled down into a single big gas cloud, whatever form it might take.
Linear momentum explains why a galaxy might be moving through space in some direction after it forms, but it does not explain its shape. For that we need a related physical law, called conservation of angular momentum. Since like linear momentum, angular momentum is conserved, whatever angular momentum the cloud had before its collapse is what it will have afterward. While momentum is related to motion through space, angular momentum is related to an object’s rotational motion, or its tendency to spin about some axis. Angular momentum is also discussed in my post about how orbits work.
The Law of Conservation of Angular Momentum
Imagine again the protogalactic cloud before it begins to collapse. It will have a large number of smaller cloudlets within it, each moving in some direction. What’s more, each of these cloudlets will have angular momentum that is related to its momentum. Unlike linear momentum, angular momentum must be measured from a particular reference point, and its value is different for different points in space. This is somewhat analogous to the way that linear momentum depends on the motion of the reference frame in which it is defined, because velocity depends upon that frame. If you don’t understand what that means, read up on Galilean relativity, or on special relativity. The takeaway point here is that the angular momentum of each cloudlet is related to both its momentum and to its position within the larger cloud.
To get a handle on all of this it will be helpful to know the definition of angular momentum. It is generally denoted by \(\vec{L}\), and it is a vector because it has a direction. I have no idea why L is used instead of some other letter.
$$ \vec{L}=\vec{r}\times\vec{p} $$
There is a little bit more to this equation than appears at first. The momentum is there, as promised, and the \(\vec{r}\) is the distance from some reference point to the moving object. The point used is arbitrary, but you will get different values of the angular momentum for different reference points. This is fine though. You just have to be sure to use the same reference point for all your computations. Then your conclusions will be valid.
If you assumed that the multiplication sign means that we multiply the two vectors, you are correct. But how do you multiply two vectors? We’ll get to that. But first, a picture will be useful to understand how these three vectors are related to one another.
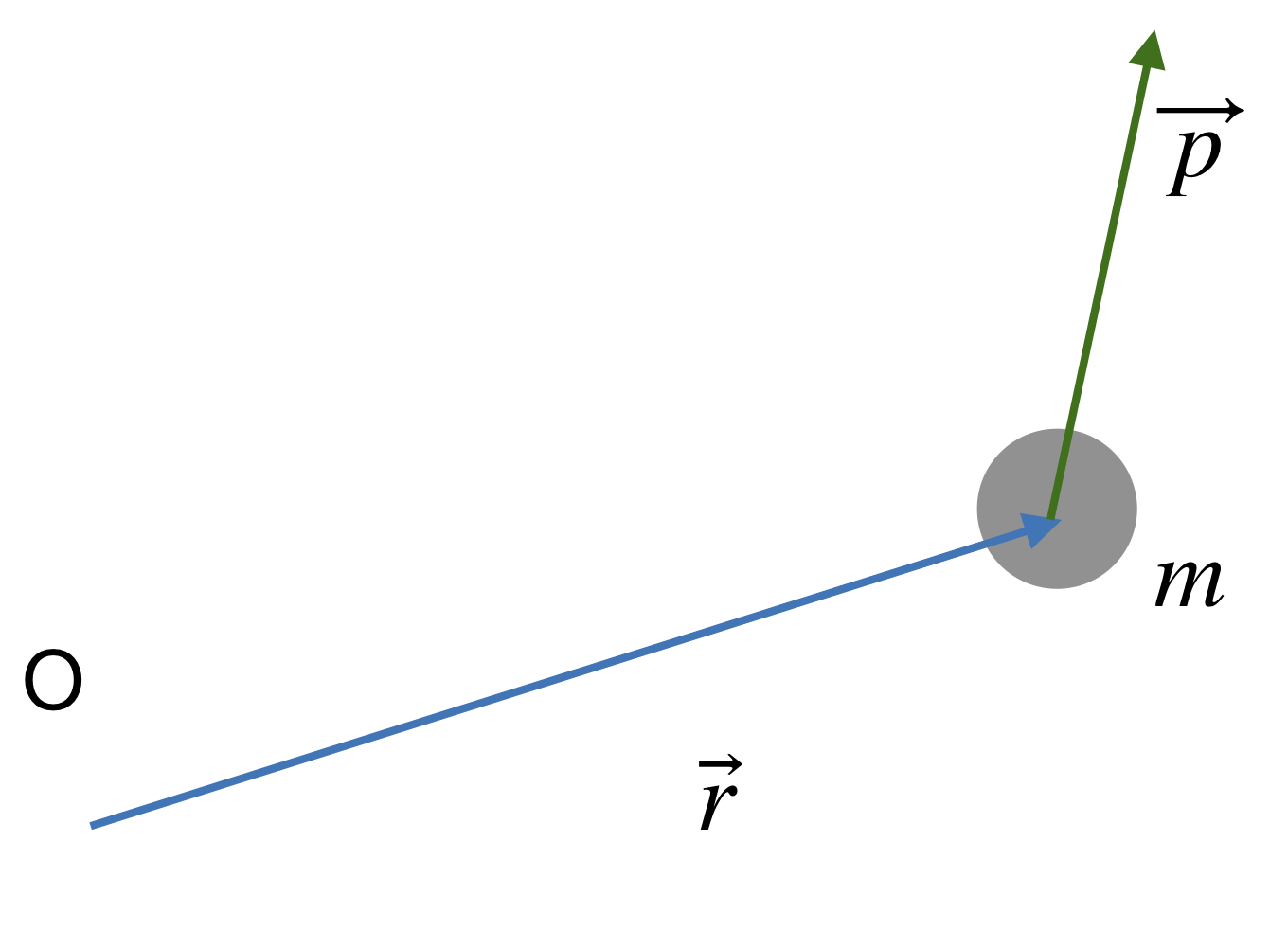
For this schematic, we are measuring the angular momentum of a particle with mass m and momentum \(\vec{p}\) that is a distance r from some point in space denoted by O. The distance vector \(\vec{r}\) has a length r (called its magnitude) and runs from the point O to the center of the moving particle. We would say that the tail of \(\vec{r}\) is at O, and its head is at the particle. Likewise, the momentum is represented by a vector (arrow) with its tail located at the particle and its head pointing off in the direction the object is moving. The length of the vector \(\vec{p}\) (its magnitude) is \(mv\). It is not a physical length or distance in space, and so the length relative to \(\vec{r}\) in this diagram has no meaning. It does have meaning when compared to other momentum vectors, just as the length of \(\vec{r}\) is meaningful when compared to other distance vectors.
To understand how we get the angular momentum from this diagram it is helpful to rearrange things somewhat, as below.

In the second diagram, we slide the r vector parallel to itself until its tail is coincident with the tail of the momentum. This is a valid thing to do because vectors remain the same if we move them around in space as long as we don’t change their length or their direction. Moving them around this way is called parallel transport, and we can parallel transport vectors around all we like, they still remain the same vectors.
After we parallel transport \(\vec{r}\) we note that it makes an angle \(\theta\) with the momentum vector. The angle will be useful below. But first, line up the fingers of your right hand with \(\vec{r}\) such that your palm faces roughly in the direction that \(\vec{p}\) is pointing. It does not have to point exactly in that direction, just in the same general direction. With this orientation, the thumb of your right hand will be pointing out of the screen. That is the direction of the angular momentum vector, \(\vec{L}\). This somewhat complicated procedure is called the right-hand-rule. Notice that if you mess up and use your left hand, your thumb will be pointing into the page, opposite of the correct answer. It is important to keep this in mind. Let’s do another example.
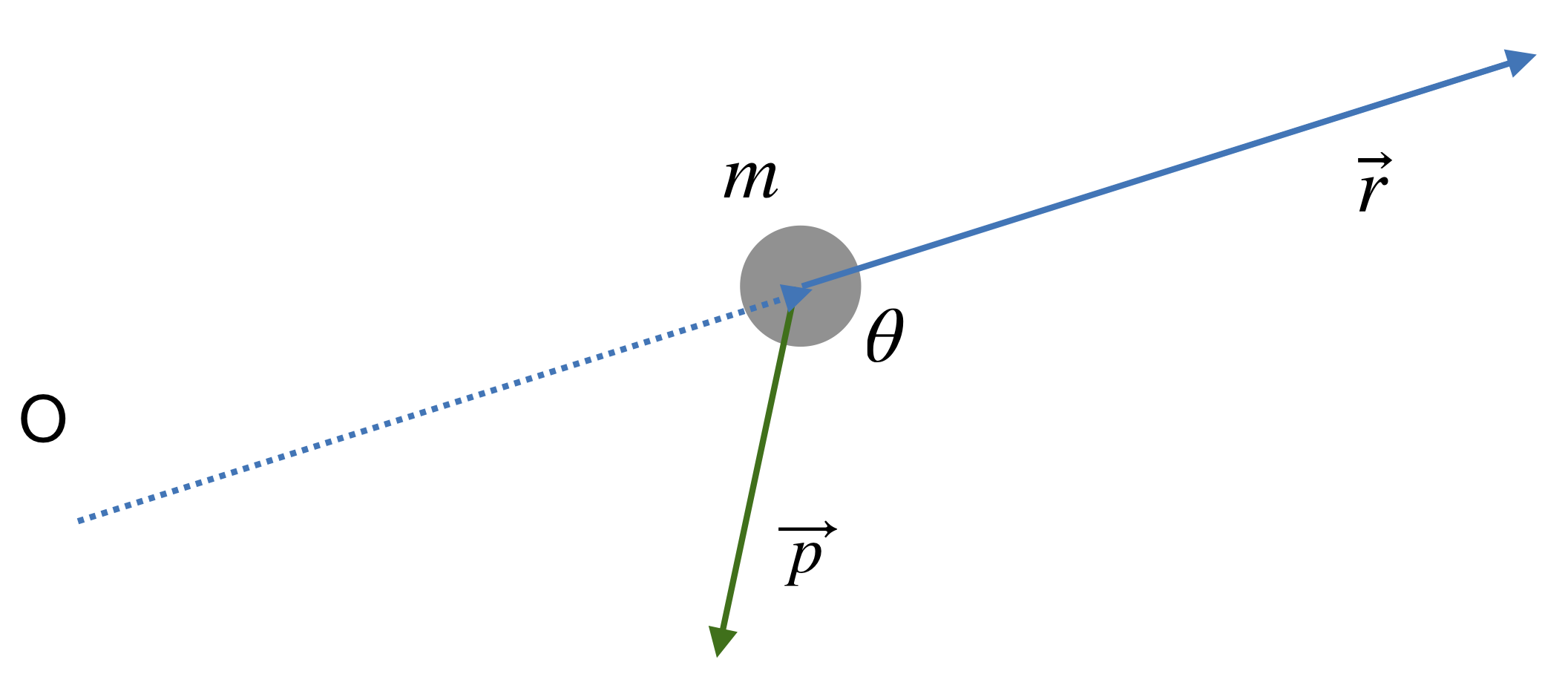
Now we have flipped the momentum vector, \(\vec{p}\), so that it points in the opposite direction from the case above; note how the angle \(\theta\) has changed in this new orientation. Use your right hand to again determine the direction of the angular momentum. You should find that it now points into the screen, opposite from your previous result. In general, if you reverse either \(\vec{p}\) or \(\vec{r}\) you will also reverse the direction of \(\vec{L}\). This is another important idea to keep in mind. Also, you must remember to always place your fingers along the direction of \(\vec{r}\) with their tips pointing in the direction the vector points, with your palm facing off in the direction of \(\vec{p}\). Never place your fingers along \(\vec{p}\) with your palm facing \(\vec{r}\). If you do, you will get the opposite answer from the correct one. Give it a try. You’ll see.
Now we have only to understand how to get the amount of angular momentum, or the magnitude of the vector \(\vec{L}\). This is given by the equation below.
$$ L= r p \sin \theta $$
The sine of an angle varies between \(0\) and \(1\), with \(\sin 0\,=\, 0\) and \(\sin 90°\, =\, 1\). This means that when \(\vec{p}\) and \(\vec{r}\) are parallel to one another, the angular momentum of the object is zero. On the other hand, when \(\vec{p}\) and \(\vec{r}\) are at a right angle, the angular momentum is maximum. At other angles the angular momentum has some intermediate value. Also, the sine (and its related function, the cosine) is a function that repeats itself. So the sine of \(180^{\circ}\) is again zero, and the sine of \(270^{\circ}\) (or \(-90^{\circ}\)) is -1. When the angle is \(360^{\circ}\) we are back at zero and the function repeats.
To get an intuitive feel for angular momentum, we can do a little thought experiment. Imagine holding a board in its middle - something you have probably done before many times. If the board is 4 meters long (about twelve feet), you could imagine holding it so that it balances on your shoulder. Imagine further that the board is a standard 2x4, or in other words that it has a cross section that is a 2 inch by 4 inch rectangle (about 5 cm by 10 cm). If you grasp the board in both hands you will find that you can rotate it quite easily about an axis that runs along its length through its center. However, if you try to rotate it through an axis that is perpendicular to its length you will have a much more difficult time. Why is this so? It is the same amount of material being rotated in both cases, so you might innocently believe that it should not matter how the board is rotated. Doubtless your experience tells you otherwise: it certainly does matter.
The difference is in how the material is distributed with respect to the axis of rotation. Material that is farther from the axis is harder to set in motion (or stop from moving) than material that is closer. That is what the factor of \(r\sin\theta\) is telling us in the definition of angular momentum. When rotating a board about an axis along its length, most of the mass of the board is relatively close to the rotation axis, so \(r\) is small. This means that the material does not acquire much angular momentum when we rotate the board about that axis. It is therefore easy to set it moving in this way. On the other hand, if we choose an axis perpendicular to the board’s length, then most of the mass is at quite a large distance from the axis. The value of \(r\) is large, and we feel the difference when we try to rotate the board. This property has to do with rotational inertia. Rotational inertial is analogous to inertia (mass) in linear motion, except rotational inertia takes into account both the amount of material moving and how it is distributed in space. In either case, we must exert effort to change the momentum (linear or angular) of an object. Left alone, objects maintain constant linear or angular momentum.
Finally, if we are holding a steel beam rather than a piece of wood, it will be much harder to rotate no matter which axis we choose to rotate around. That is why the factor of \(m\) is there - even if hidden within the \(p\). Likewise, the \(v\) hiding inside the \(p\) tells us that it is harder to make a thing spin fast than to make it spin slow. It is also harder to stop a rapidly spinning object than a slowly spinning one. Angular momentum is thus a combination of how much material is moving, how fast it is moving and how the material is distributed in relation to the rotation axis. These are all things to keep in mind when thinking about how spinning objects move. And because galaxies are spinning objects, we need to keep these ideas in mind when trying to understand them, too.
Now we are ready to show why some galaxies become disks.
Finally, A Disk!
Now we are going to imagine a large protogalactic gas cloud that, through many small collisions, forms a galaxy. For convenience, we will take the point for measuring the angular momentum to coincide with the center of mass of the protogalactic cloud. From our discussion of linear momentum above, we know that this point will move through space at a constant speed and in a constant direction, so it makes a good reference. From the vantage point of the center of mass, the cloud appears to collapse down all around us, but it does not have any bulk motion through space because we are moving along with it.
To begin, imagine extending a radius vector, \(\vec{r}\), running from the center of mass to each small cloudlet within the protogalactic cloud. These radius vectors will point out in all directions, somewhat like the spines on a sea urchin. Each will end at a cloudlet.
Then imagine the momentum vector of each cloudlet and its relation to the corresponding radius vector. In general, the momenta for the cloudlets will be distributed in random directions in space. Since the direction to each (the radius vector \(\vec{r}\)) is also random, when you use the right-hand-rule to determine the direction of the angular momentum for that cloudlet, you will find that they also are distributed randomly. So the angular momentum vectors will also resemble the spines on a sea urchin, but each will be perpendicular to the corresponding radius and momentum vectors that generate it. The total angular momentum is just the sum from all these individual clouds, as we saw for linear momentum.
$$ \vec{L}=\vec{L}_1+\vec{L}_2+\vec{L}_3+\vec{L}_4+...+\vec{L}_{n-1}+\vec{L}_n $$
The image below gives a schematic representation of what the system of cloudlets might look like - though in general there would be many, many more cloudlets (yellow ellipsoidal objects) than are shown. The radius vectors, shown in white, each start at the center of mass (the blue dot labeled C.o.M.) and run to an individual cloudlet. The momentum vector of each cloudlet is depicted in green and points in the direction the cloudlet is moving. The angular momentum vectors are not shown, just to prevent the diagram becoming too messy. They would be distributed much like the radius vectors are, except each would be perpendicular to both the radius vector and the momentum vector that generates it, as we have stated already. Keep in mind that any of the vectors shown could be pointing partially into or out of the plane of the figure: galaxies are not in general two-dimensional systems.
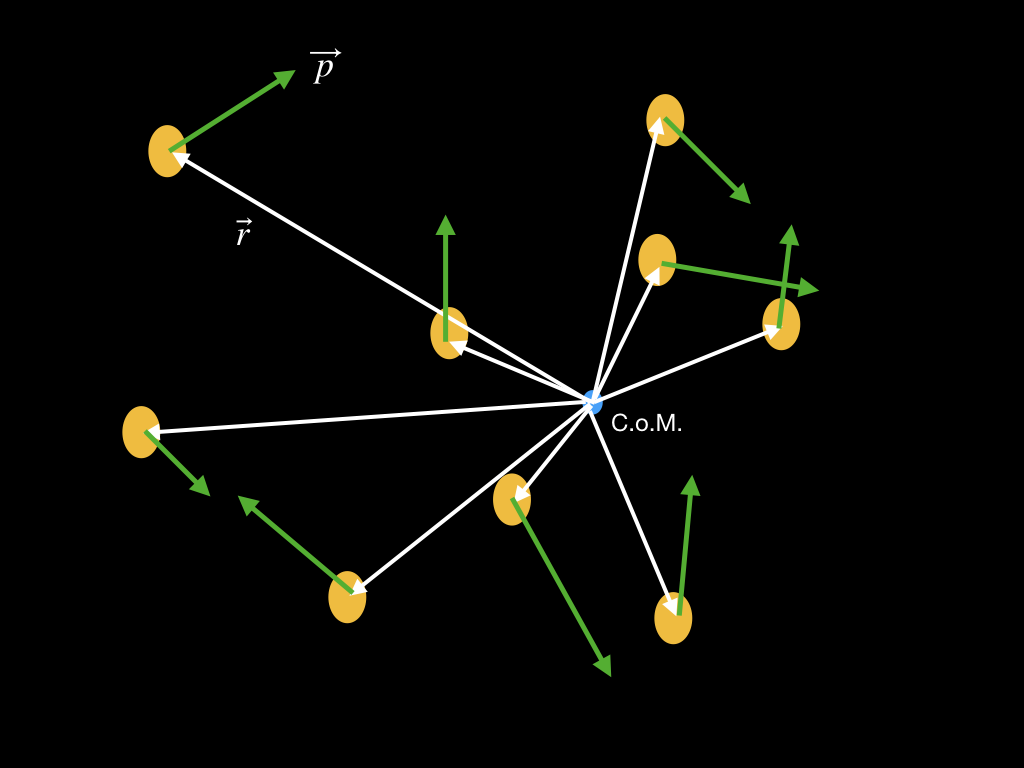
From the argument above you might conclude that there is no net angular momentum because the individual vectors point in all directions, thus canceling each other out. In fact, that is usually not the case. Most of the angular momentum vectors do cancel, but after doing the complete sum over all the cloudlets there will be almost always some amount left over that does not cancel. This is the angular momentum of the system as a whole, and it determines the orientation of the galaxy. The system will form a disk rotating in the plane perpendicular to this net angular momentum vector. The direction of the rotation, clockwise or counterclockwise, can be deduced using the right-hand-rule, as we will show in a moment.
But why a disk? Because after all the collisions have occurred, and all the cloudlets have merged, you will find that any motions that were perpendicular to the plane of the disk (or in other words, any motions parallel to the total angular momentum vector) have canceled out. On the other hand, motions that are parallel to the plane of the disk (perpendicular to the net angular momentum vector) will not have canceled. This preferred orientation in space, an oriented disk, is simply the result of conservation of angular momentum.
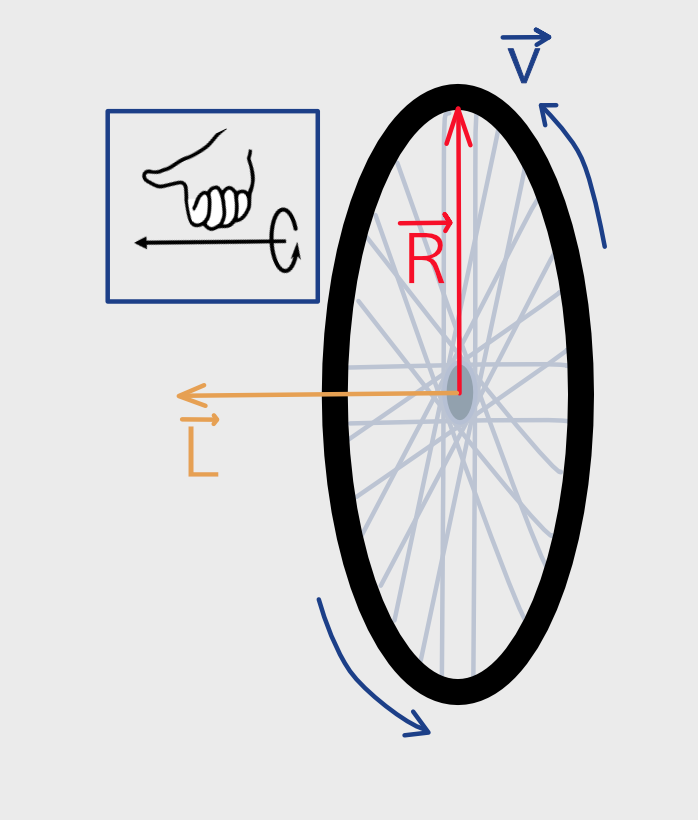
In the images below of the bicycle wheel and the galaxy, the rotation is counterclockwise in the perspectives shown. We can use the right-hand-rule, just as we did before, to understand the rotation. In this case, we use a different but related version of the rule. Curl the fingers of your right hand so that the fingers align with the direction of rotation of the disk. The method is shown in the inset box next to the bicycle wheel. With the fingers of the right hand curled in the direction of the rotation, the extended thumb points in the direction of the angular momentum. For the bicycle wheel this is off to the left, as shown. For the galaxy it is diagonally upward to the right and slightly out of the page - remember, we are assuming the galaxy rotates counterclockwise, which this particular galaxy actually does for our orientation.
The important takeaway is that the direction of the angular momentum vector uniquely determines the plane and direction of rotation. Its length is related to the amount of angular momentum of the disk, which is a combination of how fast the disk rotates, how much material is rotating and how the material is distributed within the disk. So no matter how complicated the internal motions of the protogalactic cloud were in the beginning, by the time everything has collided and settled down, the motion will reflect the initial and unchanging angular momentum of the system. The system will be a flat disk rotating around an axis aligned with the total angular momentum vector.
Galaxy Image Credit: Hubble Heritage Team (AURA/STScI/NASA/ESA)

And why are some galaxies giant balls of stars instead of disks? It has to be due to those galaxies forming stars very early in their history, before they had a chance to collapse to any great extent. Once stars form, collisions no longer happen because stars are so tiny compared to the distances between them. Even for a very large galaxy it is unlikely for two stars ever to collide with each other. Without collisions to exchange energy and momentum within the system, it cannot collapse to a disk. Instead, it remains more or less in its original extended state, as shown in the image below of an elliptical galaxy (Credit: ESA/Hubble & NASA, Judy Schmidt and J. Blakeslee (Dominion Astrophysical Observatory)).

It is difficult to get a grip on this when you consider that galaxies contain hundreds of billions of stars. Surely there must be collisions among the at least some of the time. Scaling things down to a more comprehensible size can help.
Imagine that we could shrink the Milky Way down such that the sun became the size of a grapefruit. If we placed that grapefruit in the middle of the Golden Gate Bridge in San Francisco, then the next nearest star could be represented by a grapefruit placed in the middle of the Verrazano Narrows Bridge in New York City. In between there would be no other grapefruits (stars) at all. That is how empty galaxies are. And that is why stars within them never collide. Even when galaxies collide, the stars within them do not. The gas does, but the stars pass right through, affected only by the changing gravitational field during the collision. In fact, it is probably better to refer to these galaxies as interacting, not colliding. An example of such an interaction is shown in the image below. These interactions require hundreds of millions of years to complete, or even billions of years. So the images we make of them are just a snapshot, like taking a still photograph of a ballet dancer in the middle of a jump. The fast shutter speed of the camera freezes the motion and gives the impression that the dancer is suspended in the air. In fact, we are seeing only a transient state. The dancer soon descends back to the floor; for interacting galaxies, even a shutter speed of a million years might seem instantaneous. Their interactions go on for hundreds or thousands of times longer.
(Credit: ESA/Hubble & NASA, A. Adamo et al.)

So the next obvious question is why some galaxies form stars early, and thus remain extended and spheroidal in shape, while others take a long time to form stars, and thus end up as disks. We don’t know the answer to that question. Galaxy formation is a complicated process, certainly more complicated than the simplified picture we have considered here. While the general arguments above are bound to be mostly correct, there is certainly more to the story. For instance, we know that galaxies undergo a continuous process of evolution and growth, with large galaxies subsuming smaller galaxies, or merging together to form humongous galaxies. In truth, galaxies are still forming. Whatever the detailed story, in all these ongoing formation processes, conservation of energy, linear momentum and angular momentum are foundational in determining how galaxies look today and how they will change over time.
