What Are Vectors and How Do They Work?
If you are walking along a street, in Paris for example, and a passerby stops you to ask how to get to London, you could answer that London is about 340 km away. This answer is not likely to satisfy the questioner. They would probably also want to know in what direction they should travel.
And of course, what they probably really want to know is how to get to the train station, and which train they should take. Such details are part of our contemporary existence. We are looking at underlying basic properties of the world here, so we will ignore these kinds of details.
In general, to get from one point in space to another you have to know how far away the points are from one another. But that alone is not enough. You must also know their orientation so that you move in the correct direction to travel from the first point to the second. Quantities like this, that have a size (how far in this example) and a direction (the relative orientation) are described by vectors. We will work out a few properties of vectors by citing several simple examples.
A Simple Linear Displacement
First, imagine that you are standing at some point in a two-dimensional space, on the floor of a large room like a gymnasium, perhaps. We can, for convenience, identify the point on which you stand with the origin of a standard Cartesian \(x-y\) coordinate system.
If you face toward the positive \(y\) direction and take two steps to the right, you are then standing at the point with \(x=2\), \(y=0\), or put more compactly, the point (2,0). We are assuming that each step is the same size as the gridlines of the coordinate system, and we could represent your movement by an arrow pointing from the origin to the point (2,0), as shown in the image below.
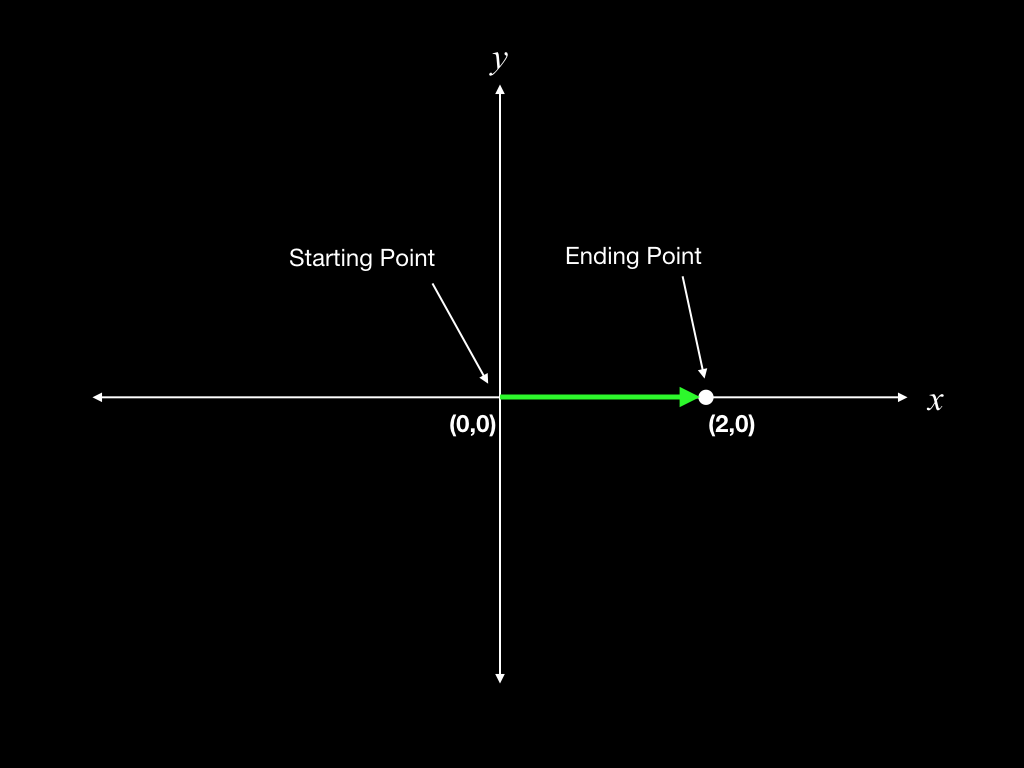
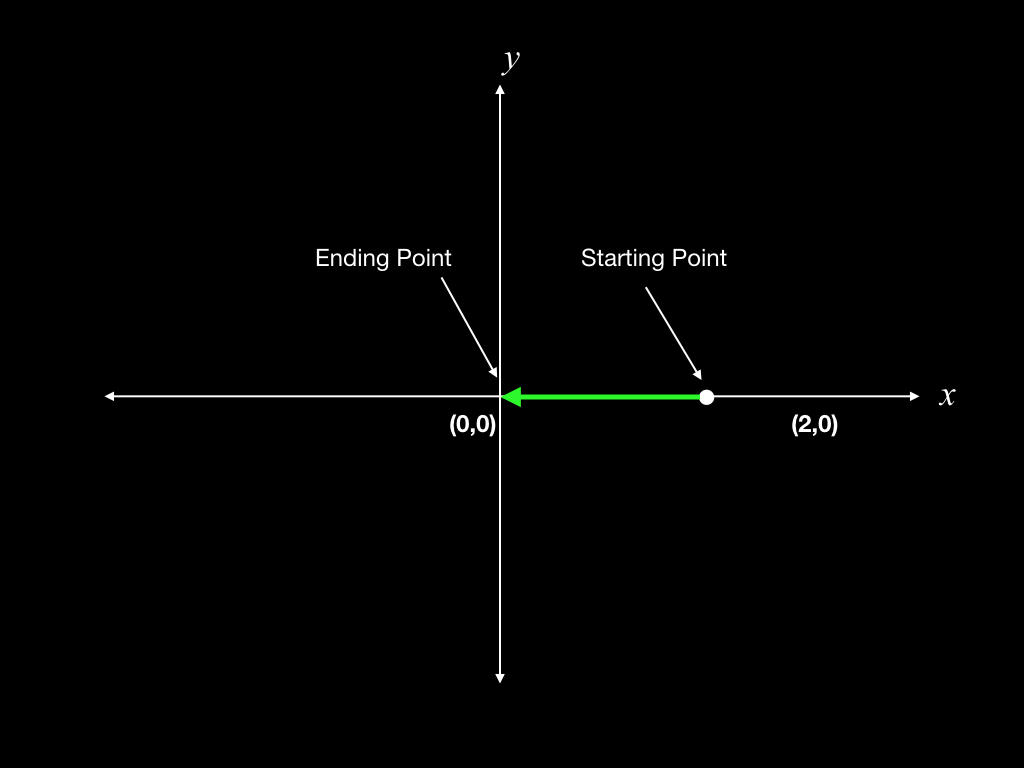
In this example, you would have traveled 2 units (steps, for the moment) of distance from where you began. If you now reverse your course and step two steps to the left you will end up where you started, at the origin. You will have traveled a total of 4 steps, two to the right, and two to the left. However, your distance from where you began, called your displacement, will be zero.
The example illustrates two different ways of thinking about distance. We can consider the total distance covered, in which case we would have passed through four steps. On the other hand, we can consider how far we are from where we started. From that perspective, our net distance traveled, or displacement, is zero. Neither perspective is right or wrong. Which of them we use depends on what aspect of motion we are interested in describing.
Going forward we will assume that each step we take carries us one meter, which is about three feet. In that case all distances will be in meters (m). Then, in the example just described you will have traveled 2 meters in the positive \(x\) direction, then 2 meters in the negative \(x\) direction. Your net distance traveled is zero meters.
This example illustrates an important aspect of vectors: they can be added to one another, but when we do so, we must take into account both their size (the length of the arrows) and their direction.
In this example, asking about the total distance traveled vs. asking about the displacement from where we started will give two different answers. You have traveled over a total distance of 4 meters, but your distance from where you began is zero. The reason is because the displacement is a vector, whereas the distance traveled is not.
Scalars and Vectors
Let’s do another example to flesh this idea out a bit more.
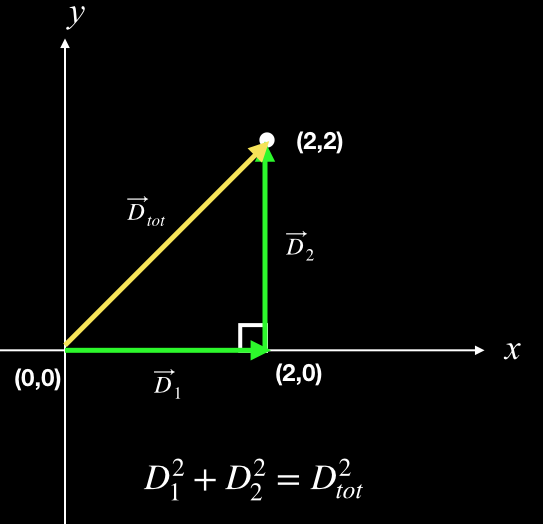
Look at the diagram below. We use it to illustrate taking first a couple steps to the right, as in our first example, and then a couple steps forward - in the positive \(y\) direction. Each of these segments of the journey is 2 maters long, just as before.
The two parts of the motion are labeled \(\vec{D}_1\) and \(\vec{D}_2\), for displacement 1 and displacement 2. Using labels like these is a convenient way of keeping them straight in our minds. As before, the total distance traveled is 4 meters, but what is the total displacement?
Well, displacement is how far away we are from our starting position, and in what direction. It can be represented by the yellow arrow in the diagram, with the label \(\vec{D}_{tot}\) for total displacement. What is its length?
Clearly, the answer is not 4 meters. We would be 4 meters from our starting point if \(\vec{D}_2\) was the same as \(\vec{D}_1\), two steps in the positive \(x\) direction. But it’s not. It is two steps in the positive \(y\) direction.
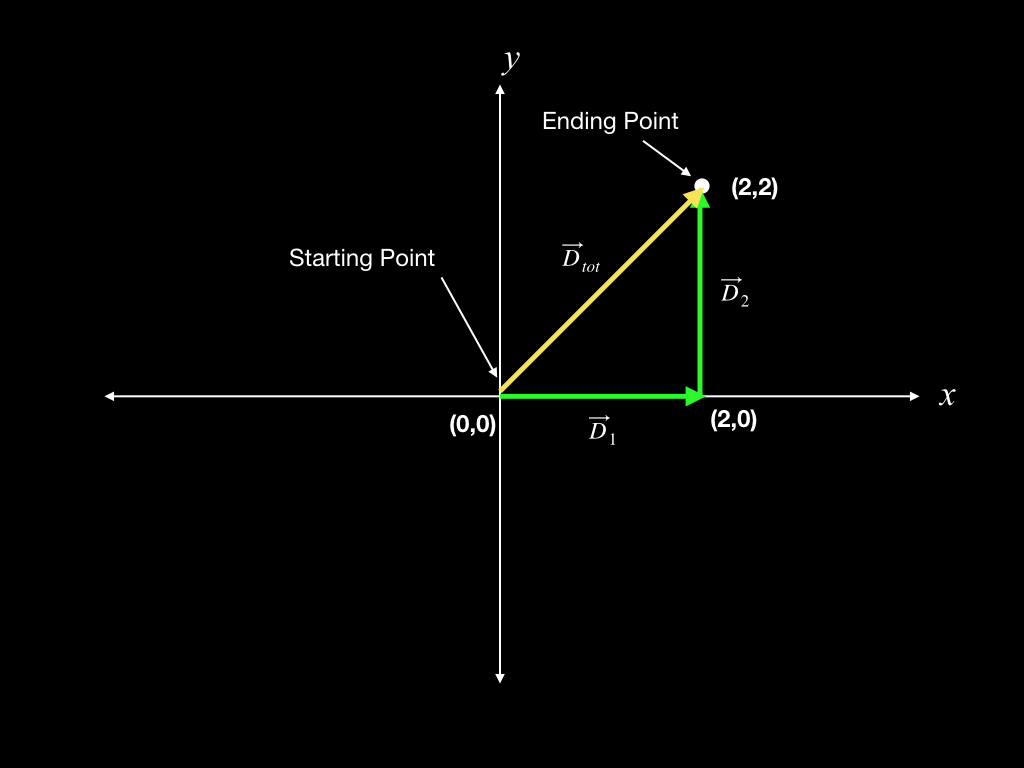
In order to find the length of \(\vec{D}_{tot}\) it helps to remember some geometry. Notice that \(\vec{D}_1\) and \(\vec{D}_2\) are perpendicular to one another, meaning they form a right angle (90 degrees) with each other. Connecting them with \(\vec{D}_{tot}\) as shown creates a right triangle with \(\vec{D}_{tot}\) as its hypotenuse. You might recall that the Pythagorean theorem relates the sides of a right triangle to each other. If not, we explain how, below.
In the diagrams below, on the left side we have a generic depiction of the Pythagorean theorem and how it relates the sides of a right triangle. On the right is our displacement diagram showing how to apply the Pythagorean theorem to it. Note that when we write \(D_1\), \(D_2\), etc., without the arrows above them, we are referring only to the length of the vectors and ignoring their direction. The length of a vector is called its magnitude, and the Pythagorean theorem can be used to relate the magnitudes of vectors to one another.
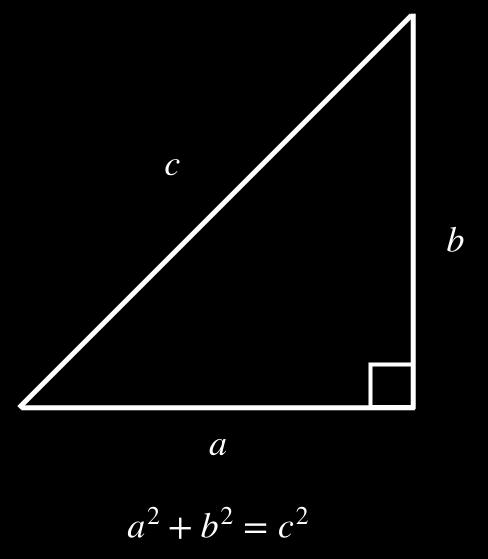
The magnitudes of both \(\vec{D}_1\) and \(\vec{D}_2\) are known. Each of them is 2 meters long. So the magnitude of \(\vec{D}_{tot}\) is given by the following.
\begin{equation}
\begin{split}
D_{tot}^2 & = D^2_1 + D^2_2 \\
& = (\rm {2\,m})^2 + (\rm{2\,m})^2\\
& = \rm{ 4\,m^2 + 4\,m^2}\\
& = \rm{ 8\,m^2}
\end{split}
\end{equation}
or, taking the square root…
\begin{equation}
D_{tot} = \rm{ \sqrt{8}\,m = 2\sqrt{2}\,m \approx 2.828\,m}
\end{equation}
Notice that when we square the magnitude of a vector, we must square its units, too. In this case the units are meters, so we have meters squared: \(\rm{m^2}\). But that’s okay because we take the square root at the end to get back to just meters, as we expect for a distance or length.
We have found that, after taking two steps to the right and two steps forward, assuming each step is one meter long, we have traveled a net distance equal to almost three meters from where we started. We have traveled a total of four meters to get three meters away. That is not very efficient. This is why it is generally faster to travel directly between points along a straight line. This assumes there is not a mountain, cliff, lake, etc, along that direct path.
We are not going to consider those real-world details here. In an ideal simplified world, one without geographical barriers, the most efficient (and usually quickest) way to get from point A to point B is to follow the straight-line path connecting them.
Quantities like distance are called scalars. They are simple numbers with no direction associated with them. In this example, we have traveled a distance of four meters - a scalar - to get 2.82 meters from where we started. This 2.82 meters is also a scalar until we put a direction to it. When we include the direction it becomes a displacement, a vector.
From the diagram we can see that the angle made by \(\vec{D}_{tot}\) is \(45^{\circ}\), so we can say that the vector \(\vec{D}_{tot}\) is 2.82 meters at \(45^{\circ}\) above the positive x-axis. There are other ways to specify the vector, but this is good enough for our current discussion.
One more example will help clarify in our minds how vectors work.
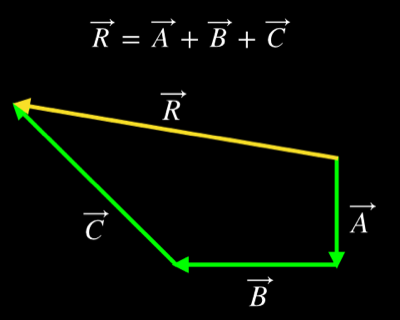
Addition of Vectors
The example above shows how vectors are added in general. Any two vectors can be added together by placing the tail (or base) of one at the head (point of arrow) of the other. The resulting vector is found by placing its tail at the tail for the first vector and its head at the head of the second. Notice this is how we have added \(\vec{D}_{1}\) to \(\vec{D}_{2}\) in order to find \(\vec{D}_{tot}\).
If there were a third vector, it could be added in by placing its tail at the head of \(\vec{D}_{2}\) (or \(\vec{D}_{tot}\)). The resultant would then be found by running a vector from the tail of \(\vec{D}_{1}\) to the head of this third vector. Any number of vectors can be added this way.
Two things to keep in mind when adding vectors: First, you can imagine moving any vector all around. As long as you change neither its direction nor its length, you do not change the vector. This is called parallel transport. If you do change either of those, then you have changed the vector.
Additionally, all the vectors added together must be of the same type. It doesn’t make any sense to add a length vector to a momentum vector. You can only add length to length, momentum to momentum, force to force, etc. This works the same with scalars; you would never add a mass (kg) to a time interval (seconds). What would kilograms plus seconds give you? If you don’t know, well, I don’t either!
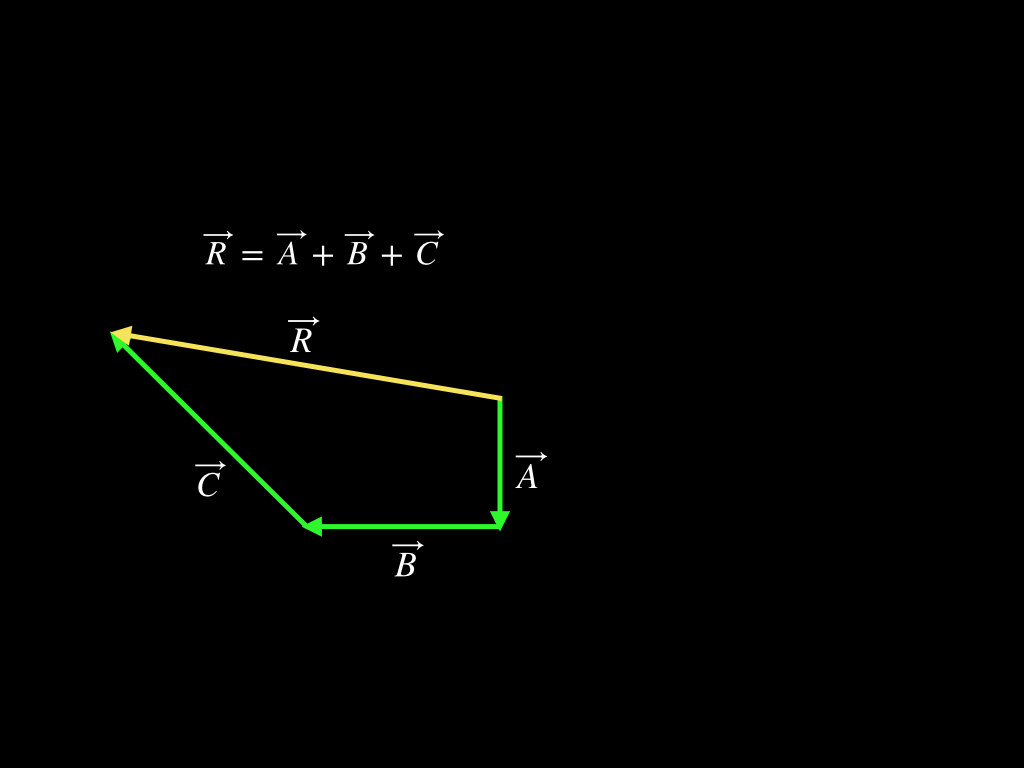
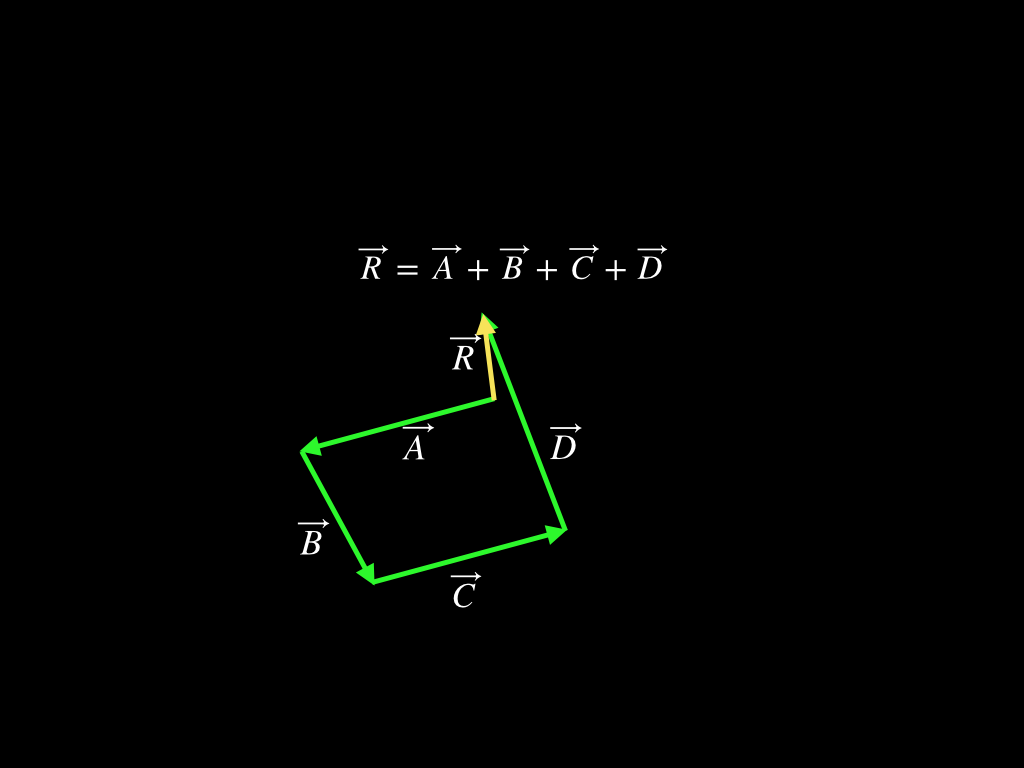
The schematics below show two examples for adding vectors, tail to head, to find a resultant vector (their vector sum). In each case, the initial vectors to be added are on the left, and the rearrangement and resultant vector are shown immediately at right. Note that in each case, the vectors to be added are moved around and placed tail-to-head, but their directions and lengths always remain the same.
These diagrams, while accurate, are meant to be conceptual. When actually carrying out the mathematics we have to be more sophisticated and use vector components. The procedure is similar to what is shown above, but the details would take us too far into the weeds. If you want to know more about this topic, consult an introductory level physics text for high school or college.
Vectors to Add
Resultant Vector
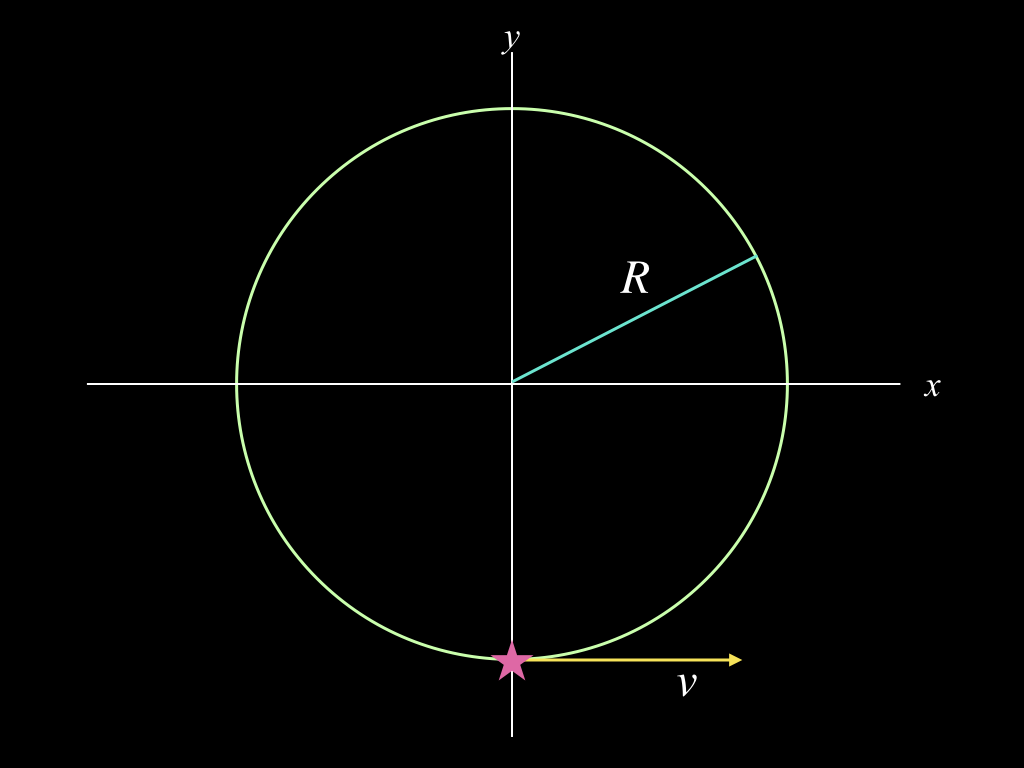
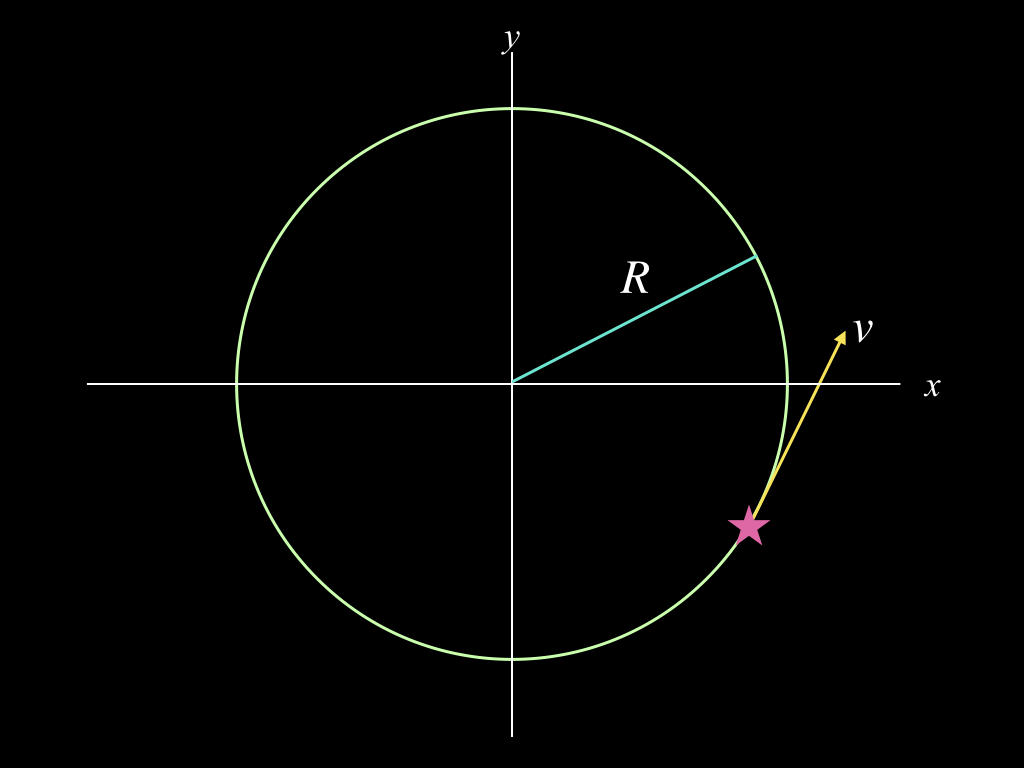
Motion Along A Circular Path
Imagine an object, represented by the small purple star, is moving along a circular path with a constant speed, \(v\). The radius of the circle is \(R\). Such a system is depicted in the diagram below for two distinct times. At any instant, the motion of the object is a vector (represented by the yellow arrows) that is tangent to the circle at the position of the object at that particular moment.
The magnitude of this vector (its length) is proportional to the speed at which the object is moving. Since the object moves in a circle, its motion constantly changes. Even if it has a constant speed, the direction of its motion is never the same from one moment to the next. So the instant shown at the left could be a few moments before the one shown on the right. As the object moves around the circle, the direction it is moving continuously changes.
You will probably not be surprised to know that its motion is represented by a vector. That vector is called the object’s velocity. It is distinct from the object’s speed. If you have guessed that the speed is the magnitude of the velocity, you are correct.
Same as with distance, speed alone does not give us a complete picture. We need to know the direction of motion for that, and so the velocity. Speed and velocity share the same relationship to one another as do distance and displacement.
Suppose that the object in the diagram requires one minute to go all the way around the circle. We would say its motion has a period of one minute. Let’s further stipulate that the size of the circle over which it moves is 10 meters across. In that case we know that its speed is given by the distance over which it travels divided by the time taken to complete the trip. If we label the circumference of the circle as \(C\) and the time required to travel around one time \(T\), then we can write the following equation for the speed, \(v\). Note we use a letter \(v\) without the arrow because the speed is the magnitude of the velocity vector.
\begin{equation}
\begin{split}
v & = \frac{C}{T}\\
& = \frac{2\pi R}{T}\\
& = \frac{(2\pi)(\rm{5\,m}) }{\rm 60\,s}\\
& \approx \rm{0.52\,m\,s^{-1}}
\end{split}
\end{equation}
So this object is traveling about half a meter per second. If it travels 60 seconds we would expect it to have moved about 30 meters, but in fact after a single trip around the circle it has not moved at all from where it started. This is because its average velocity over its trip is zero.
It’s average speed, however, is \(\rm{0.52\,m\,s^{-1}}\). How can they be different? Because as the object moves around the circle, its velocity rotates through an entire \(360^\circ\) arc, so cancels to zero.
To understand how this can be so, imagine paring the velocity at every point along the circle with the velocity at the point on the opposite side of the circle. These velocity pairs will be equal in length but opposite in direction. They will add to zero as a result. What is more, every point along the path can be paired this way, so the vector sum of all the velocities along the path must be zero. Thus the average velocity over the entire path must also be zero.
However, the speed has no direction associated with it. Instead, it is simply a constant number, about half a meter per second. The average value of a constant is simply its constant value. This example illustrates the fundamental difference between a vector, like velocity, and a scalar, like speed.
A few examples of vectors and scalars that are fairly common are given below. You might not be familiar with all of these, but that is okay. Consider the items you do know. Do you understand why they are classified either as scalars or vectors?
Vectors
Displacement
Velocity
Acceleration
Force
Momentum
Angular momentum
Gravitational field
Electric field
Magnetic field
Scalars
Distance
Speed
Area
Volume
Mass
Density
Electric charge
Pressure
Time
Work
Energy
Entropy
Temperature
If you consider all of the objects on the left, you will realize (assuming that you are familiar enough with them) that they have a direction associated with them, not just a size. The items on the right do not. They have only size, but no direction.
As we have seen, vectors have some interesting mathematical properties. The important takeaway is that vectors have both a size and a direction: you can think of them as arrows of a certain length pointing in a certain direction. When you add vectors together you cannot just add them as if they were numbers. You must take into account their direction. You must also make sure that you are adding vectors of the same type, so displacement to displacement, force to force, acceleration to acceleration, etc. This is also true for scalars, of course.
If you are wondering if you can multiply vectors, you can. Again, you have to be careful when you do it, and take into account that they are vectors, not numbers. A discussion of how to multiply vectors is a bit more than we want to bite off here, so I’ll just tell you that there are two ways to multiply them. In one way the result of the multiplication is a scalar. In the other way the multiplication results in a vector.
If you want to know how this works, have a look at an introductory college level physics textbook. There you will find a much more thorough discussion of vectors and their properties. You can also learn how to multiply vectors, and explore a more complete discussion of how to add them together. We have only touched on the most basic ideas here.