Why Do Astronomers Think There is Dark Matter?
The evidence for dark matter goes back to the 1930s, or even further if we broaden our meaning somewhat. For example, people long thought that there was a planet in close proximity to the Sun, even closer than Mercury. They thought this was true because Mercury had unexplained perturbations in its orbital motions,. Put another way, Mercury did not follow the predictions of Newton’s laws of gravitation and his laws of motion. One possible explanation for the discrepancy could have been that the laws were simply wrong. But they worked for other objects, so why not for Mercury?
To understand why these discrepancies are a problem, we have to know what Newton’s laws are. We’ll begin with the Law of Universal Gravitation. If you already understand Newton’s laws, you can skip the next couple of sections.
Newton’s Law of Gravitation
Newton’s law of gravitation describes the force that one object exerts on another due to the gravitational effect. It says that the force is proportional to the product of the masses of the two interacting objects. In other words, the bigger the product of the masses, the bigger the force exerted. It doesn’t matter if there is one large object and one small one, or if both objects have the same mass. As long as the product of the masses is constant, the force exerted will be the same.
The force also depends on the distance separating the two objects, and it becomes smaller as the objects get farther apart. However, it does not diminish in a simple linear fashion. The force is inversely proportional to the square of the distance between the two. The “inversely” part means that the force involves the reciprocal of the distance, but the “square of the distance” part means that we have to use the square of the distance, not the distance itself.
Mathematically we can write all of these dependencies as is done below.
$$ \vec{F_{12}} = -\frac{G m_1 m_2 }{r^2}\hat{r} $$
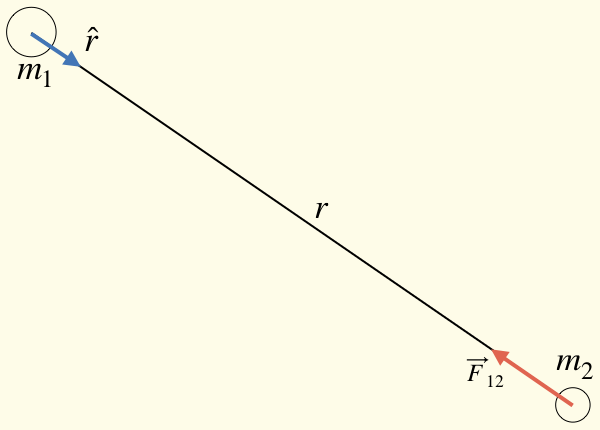
This equation provides the force \(\vec{F}_{12}\), meaning “the force of object 1 upon object 2.” The symbols \(m_1\) and \(m_2\) are the respective masses of the objects, and \(r\) is the distance separating them. The small arrows above the \(\vec{F}_{12}\) and the \(\hat{r}\) remind us that the force is a vector quantity; it has both a size and a direction. In particular, \(\hat{r}\) is called a unit vector because it has unit length, or in other words, a length of 1. It has no units of measure (no meters or inches or anything like that) and is there only to provide a direction; it always points along the radial direction in a polar coordinate system centered on one of the objects and toward the other object. The negative sign tells us that the direction of the force is opposite to the radial direction for a coordinate system centered on that mass. A picture will probably make this more clear.
The diagram below at left depicts the geometry. It shows \(\vec{F}_{12}\), the force that object 1 exerts upon object 2. Note that the coordinate system is centered on the first object. That is why the unit vector \(\hat{r}\) begins there and points toward object 2. The force felt by object 2 from the gravity of object 1 (\(\vec{F}_{12}\) ) is directed along the same line, but it points in the opposite direction. As is customary, the force acting on object 2 is shown at object 2, but like any vector, it can be moved around as we like. As long as we don’t change either of its length or direction, we do not change the vector.
A similar diagram could be used to show the force that object 2 exerts on object 1. We could call this force \(\vec{F}_{21}\). The force is depicted in the diagram on the right. The two forces are equal in strength and opposite in direction, and so \(\vec{F}_{21} =- \vec{F}_{12}\) (see Newton’s Third Law, below). This fact is also clear because we do not change the strength of the force by changing the order of multiplication of the masses in Newton’s gravitational law: \(m_1 m_2 = m_2 m_1\).
The symbol \(G\) in Newton’s law is called the gravitational constant. It keeps track of the system of units we are using to measure distance, mass and force. In the SI system of units (mass in kilograms, distance in meters, force in newtons) the gravitational constant has the numerical value below. For other systems of units (measuring force in pounds, distance in feet, etc.) it will generally have a different value.
$$ G = 6.67 \times 10^{-11}\rm\, N\,m^2\,kg^{-2} $$
One thing to note in passing is the tiny value of \(G\). The \(10^{-11}\) is a very, very small number. It means that in order to get an appreciable force we need to have a lot of mass. Alternatively, we could place the masses exceptionally close together so that \(r\) is small. As an example, if we have two \(\rm 1\,kg\) masses that are \(\rm 1\,m\) apart, we get a force so small as to be completely negligible in most cases.
$$ F = \frac{\rm (6.67 \times 10^{-11}\rm\, N\,m^2\,kg^{-2})(1\,kg)(1\,kg) }{(\rm 1\,m)^2} = 6.67 \times 10^{-11}\rm\, N $$
An example you can try yourself is to calculate how close these two objects would have to be to create a force of 6 or 7 newtons between them. You will find that it is quite a small number; compare it to the average distance between the proton and electron in a hydrogen atom, which is about \(\rm 10^{-10}\,m\).
As far as we can tell, this law works everywhere in the universe. Well, almost everywhere. We’ll get into some of that later. In particular, it should describe the motions of all the planets as they orbit the Sun, it should describe the motion of the Moon orbiting Earth, it should describe the motion of a rock falling on the surface of Earth. All of these motions are dominated by gravity to the extent that other forces, like air resistance from Earth’s atmosphere, for example, can be neglected. These non-gravitational effects can be neglected for rocks that are not falling too fast, but we cannot ignore them for falling feathers or pieces of paper. They should certainly not important for the motions of objects in outer space.
Newton’s Laws of Motion
In addition to his Law of Universal Gravitation, Isaac Newton formulated three Laws of Motion. These laws describe all the motions of all bodies we observe around us, at least in the classical view of the world. They break down when we try to use them to describe atomic or subatomic particles, or when we attempt to use them to predict the motion of bodies traveling close to the speed of light. For those special (but often important) conditions we need new physics as revealed by The Special Theory of Relativity or by quantum mechanics. For all other situations, Newton’s framework works exceedingly well. We briefly state each of his laws below, and then we explain their general meaning in what follows.
Newton’s First Law of Motion:
An Object in motion moves in a straight line at constant speed unless acted upon by a net force.
Newton’s Second Law of Motion:
The net force exerted on an object, or in other words, the sum of all the forces acting on it, is equal to the product of its mass and acceleration. Or mathematically:
\(\vec{F}_{net}=m\vec{a}\)
Newton’s Third Law of Motion:
Every force exerted by one object upon a second induces an equal and opposite reactive force exerted by the second upon the first.
In addition to his Law of Universal Gravitation, Isaac Newton formulated three Laws of Motion. These laws describe all the motions of all bodies we observe around us, at least in the classical view of the world. They break down when we try to use them to describe atomic or subatomic particles, or when we attempt to use them to predict the motion of bodies traveling close to the speed of light. For those special (but often important) conditions we need new physics as revealed by The Special Theory of Relativity or by quantum mechanics. For all other situations, Newton’s framework works exceedingly well. We briefly state each of his laws below, and then we explain their general meaning in what follows.
Motion in a Gravitational Field
All of the laws of motion are generally true for any force, but the second law allows us to make quantitative predictions in specific situations. For example, we can use it to analyze the motion of objects under the influence of gravity alone. All we have to do is set the force, \(\vec{F}_{net}\), in Newton’s Second Law equal to the gravitational force, as below.
$$ m_2\vec{a_2} = -\frac{Gm_1m_2}{r^2} \hat{r}$$
Note that the subscripts here have a formal meaning. On the left we are using Newton’s Second Law to write the net force on mass 2. Further, with the equal sign we are saying that this (net) force is the same as the gravitational force between mass 1 and mass 2. This equation can be simplified in a number of ways in order to make its meaning more clear. First, we can cancel the common factor of \(m_2\) by dividing both sides of the equation by that value. In addition, we can remove the vector signs and the minus sign. All these do is remind of of the direction of the acceleration, and that it is opposite to the direction of the unit vector \(\hat{r}\). But we know that the acceleration of object 1 points directly at object 2; we are dealing with an attractive force that always acts along the line connecting the two gravitating bodies, so the direction is not in question. What we are really interested in, as a result, is just the strength of the force.
Finally, we will rename the mass \(m_1\) to a capital \(M\). Since we have rid ourselves of \(m_2\), we don’t really need to keep the subscript 1 on the mass of object 1. It just makes our notation redundant and cumbersome, so we will get rid of it. What’s more, using an upper case \(M\) for the mass creating the gravity is a common convention, and we will follow it. This does not change anything, it just replaces the name we are using for the mass of the object creating the gravitational field that accelerates the second mass. After these simplifications, the equation can be written as below.
$$ a = \frac{GM}{r^2} $$
A Brief Aside for Clarification
While we have assumed that object 2 is orbiting in the gravitational field of object 1, we could have done the opposite. In fact, the objects each orbit in the gravitational field of the other. So, for example, as Earth orbits Sun, it is also true that Sun orbits Earth. More accurately, we should say that they both orbit their common center of mass. Because the Sun contains so much more mass than Earth, the center of mass of the Earth-Sun pair is nearly coincident with the center of the Sun. So in this particular example the distinction is not usually important. That is not true for objects of more similar masses. Two stars in a binary system is one example. If the stars have the same mass, then the center of mass of the system is halfway between the two. In that case, the stars orbit - that is, they follow paths centered on - a point in space that is completely empty. This small detail is a good thing to keep in mind when thinking about gravity. Do not make the mistake of thinking that less massive objects “orbit around” more massive ones. In fact, according to Newton’s law, all objects with mass produce gravity, and all objects with mass respond (that is, they move) in response the gravitational field produced by other objects. It’s just that objects with more mass move less than objects with less mass. This effect has been used by astronomers to detect planets around other stars as they undergo small motions under the influence of the gravity of the planets orbiting them.
The equation above gives the gravitational acceleration caused by an object with a mass \(M\) located a distance \(r\) away. It is often called the gravitational field and denoted by a lower case \(g\). We can use it, to take one example, to compute the surface gravity of Earth, which has a mass of \(\rm 5.98\times 10^{24}\,kg\) and a radius of \(\rm 6378\,km\). Note that to do the calculation we must convert the radius from kilometers to meters.
$$ g = \frac{\rm (6.67\times 10^{-11}\,N\,m^2\,kg^{-2})(5.98\times 10^{24}\,kg)}{\rm (6.378\times 10^6 \,m)^2} = \rm 9.81\,m\,s^{-2}$$
This is the value of Earth’s surface gravity, a number first measured by Galileo more than 400 years ago, though he expressed it in different units, of course. It is the same for all falling objects regardless of their mass (or their “weight” if you prefer, though be careful: weight and mass, while related, are not the same). While it’s true that more massive objects feel a larger force from gravity (Newton’s gravitational law), they also have a larger inertia, and so are more difficult to accelerate (Newton’s Second Law). The two effects exactly cancel each other, and so all objects fall at the same rate, regardless of their mass.
We should point out here that we might have pulled a little bit of subterfuge above. To understand how, consider the following: Newton’s gravitational law essentially gives us a definition of a quantity we could call gravitational mass. It depends only upon the gravitational interaction between two massive bodies. The Second Law is a definition of something we might call inertial mass. It describes how an object’s acceleration depends on its mass and the force exerted on it. We set them equal in our analysis above when we canceled the \(m_2\) in the Second Law with the \(m_2\) in the gravitational law. There is no reason that the two have to be the same, and there are some theories of particle physics that predict small differences between them. Experiments have been run in an attempt to measure these possible differences, but so far, no differences have been found. Maybe that is because there actually are no differences, or maybe it is because our current experiments lack the sensitivity required so measure them. In any case, it is something to keep in mind as you continue to read through this post. All of its conclusions depend upon the equivalence of gravitational and inertial mass.
You might also have objected to the distance we used in our computation above. If we stand upon the surface of Earth, then the distance to the Earth is not the same as the distance from its surface to its center. It’s zero! While that is certainly true, it is also true that, gravitationally speaking, the distance that matters is the distance to the center. That is because a spherical object like Earth has a gravitational field outside its volume that is identical to that of an object with the same mass located at a point at its center. Newton was the first person to prove this assertion mathematically. If you are curious to know how the proof works, have a look in an introductory calculus-based text on physics. In any event, Newton’s gravitational law describes the gravitational force between any two such point masses, so our computation turns out to be the acceleration created by a point-Earth located at the center of the actual Earth. The treatment is valid (to very good approximation) anywhere outside Earth’s volume.
The result above gives a theoretical underpinning to Galileo’s discovery that all objects fall at the same rate when under gravity’s sole influence. Galileo had conducted experiments to arrive at his conclusion, but it was not until Newton proposed his laws of motion and gravitation that the phenomenon was understood theoretically.
We could repeat this same calculation for all the planets, for the moon, or basically for any point in space. For example, we could compute the value of Earth’s gravitational acceleration at the distance of the Moon. We would only have to replace the radius of Earth with the distance from Earth to the Moon. This distance is 384402 kilometers. You can substitute this value for Earth’s radius, above, if you like. Then you will see how fast the Moon is falling toward Earth. Just don’t forget to convert from kilometers to meters before you do the substitution. If you neglect this step, your answer will be off from the correct one by a factor of 1000 squared, i.e., a million!
Circular Motion
We are now ready to explore how the mass of an object can be determined by observing the gravitational effects it has on another object. Recall that, according to the First Law of Motion, an object moves in a straight line at constant speed unless it is acted upon by a net force. So if the object either speeds up or changes direction, then there must be a net force acting. Let us use this idea to find a means to measure the mass of gravitating objects.
To begin, consider one of the planets orbiting the Sun. The planets’ orbits are slightly distorted from a circle; they are ellipses, of which a circle is a special case. However, their orbital paths are close enough to circular that we do not make a large error by assuming they are perfectly circular. Certainly our reasoning will still be valid, even if our mathematical results will be in slight disagreement with reality.
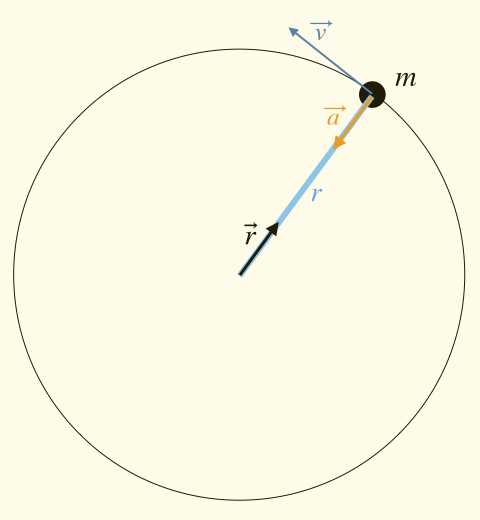
A general result from Newtonian mechanics is that an object moving at a constant speed along a circular path has a constant acceleration, called the centripetal acceleration. Centripetal means center-seeking. This acceleration does not cause the moving object to speed up or slow down, it only changes the direction of the object’s velocity. Further, the acceleration vector points toward the center of the circular path (in the minus \(\hat{r}\) direction), so it really is center seeking. We have a somewhat more detailed discussion of this in the blog post What is an Orbit?
The mathematical expression for the centripetal acceleration is shown below. The acceleration is shown with a subscript \(c\) to emphasize that we are specifically referring to centripetal acceleration.
$$ \vec{a}_c = -\frac{v^2}{r} \hat{r} $$
The figure below shows the geometry. An object with mass \(m\) moves along a circular path with radius \(r\). The object moves at a constant speed, and at each point along the path the velocity is tangent to the path, as shown by the vector \(\vec{v}\). The radial unit vector, \(\hat{r}\), always points from the center of the circle outward toward the position of the object at any particular moment in time. The acceleration vector \(\vec{a}\) points inward from the object toward the center, opposite the direction of \(\hat{r}\).
For a planet in orbit about the Sun, the centripetal force is provided by the Sun’s gravity. That means we can set the centripetal acceleration equal to the gravitational acceleration in this case. We then arrive at the following expression, in which the relationship between the motion of the orbiting object (its speed, \(v\)) to the mass of the gravitating body is becoming clear. In this case, the mass of the gravitating body is \(M\), the mass of the Sun.
$$ \frac{v^2}{r} = \frac{GM}{r^2}$$
There is a common factor of \(r\) in the denominator of both sides of this equation. We can therefore simplify things by multiplying the entire equation by \(r\), canceling the factor on the left and leaving only a single factor on the right. We then have the expression below.
$$ v^2 = \frac{GM}{r}$$
We now see the relationship between motion and mass quite clearly. An object with greater mass causes an orbiting object to move faster than a lower-mass object does. Keep in mind, we are referring to the mass of the object creating the gravity, not the mass of the orbiting object. So for the solar system, we consider that the Sun is creating the gravity. The planets are orbiting in the gravitational field created by the Sun. The mass of a given planet does not matter: for a given orbital radius, a planet of any mass will orbit at the speed given above. Additionally, as the orbit gets bigger (as \(r\) increases) the velocity gets smaller. So planets farther from the Sun move more slowly than planets near to the Sun, the mass of the planet notwithstanding.
We can find exactly what we want, the mass in terms of the velocity, by rearranging. If we multiply the equation by \(r\) and divide by \(G\), we then have a final equation that gives the mass in terms of the (presumably) measurable speed of the orbiting object.
$$ M = \frac{v^2 r}{G} $$
This equation provides the mass of a gravitating object in terms of the affect it has on the motions of objects near it. In particular, we can use it to determine the mass of the Sun if we know the orbital speed of any of the planets. And we do.
The speed of Earth in its orbit is about \(\rm 30\,km\,s^{-1}\), which we can determine by noting that it’s orbital radius is 149 million kilometers, and it requires a year (365.26 days) to orbit one time. Using these numbers and plugging into the expression above gives us the mass of the Sun. We have, of course, remembered to convert the orbital radius from kilometers to meters and the orbital period from days to seconds.
$$ M_\odot = \frac{\rm (3\times 10^4\,m\,s^{-1})^2 (1.49\times 10^{11}\,m)}{\rm 6.67\times 10^{-11}\,N\,m^2\,kg^{-2}} = \rm 2\times 10^{30}\,kg$$
We could repeat this calculation for each of the other seven planets, plus asteroids, etc. Each would give the same answer for the mass of the Sun to within uncertainties. Of course, we remind ourselves that the planets are not on circular orbits. They follow ellipses, and this contributes to some of the variation we would get. However, it is illustrative of the methods used to measure the masses of objects in space. More sophisticated mathematical treatments yield better mass determinations, and they follow along essentially the same lines of reasoning. Namely, motions of objects in a gravitational field can be used to infer the mass of the object producing the gravity that is affecting the motion of the orbiting bodies.
So what does all this have to do with the orbit of Mercury, and what does that have to do with dark matter? Everything.
If we know the mass of the gravity source, we can predict the motions of objects in that gravity field. On the other hand, if we can observe the motions of objects in space, we can infer the mass that must be present to produce those motions. Both effects play into the observations of Mercury’s orbital motions.
The Puzzle of Mercury’s Orbit
It was long known that Mercury’s orbit does not follow the predictions made by Newton’s laws. The mass of the Sun was well known because of calculations like the one above, therefore it should have been possible to accurately predict the motion of Mercury. However, this was not the case. Mercury exhibited very small, but quite noticeable, differences in its orbit from those predicted by Newtonian gravity. It was assumed that there must be some extra gravity causing its motions to be perturbed. The source of this extra gravity was postulated to be an unseen planet, and the planet was given the name Vulcan. Astronomers searched for Vulcan in the twilight sky for many years. (Mercury is always near to the Sun, and so only visible in twilight. So would be the case for Vulcan.) Despite the most careful searches, no solid detection of Vulcan was ever made. Several false alarms were reported, but they always evaporated upon further observations. To this day there has not been a planet seen between Mercury and the Sun. Apparently, Vulcan does not exist.
So, how was the issue of Mercury’s strange orbital motion finally solved? It took a new and better understanding of gravity. In other words, new physics was needed. This was provided by Albert Einstein in 1915 with his Theory of General Relativity. In fact, the first test Einstein made of his new theory, before he had even announced it, was to use it to compute the orbit of Mercury. The results of his calculations matched Mercury’s motions exactly.
In regions where gravity is strong, like in the vicinity of the Sun (where Mercury orbits) General Relativity (GR) gives slightly different predictions for the motions of objects than Newton’s laws do. It turns out that GR is more accurate in these regions. Where gravity is weaker, the two theories give the same predictions. In fact, when gravity is weaker, GR, which is an extremely difficult theory mathematically, simplifies to become mathematically equivalent to Newtonian gravity. It is only when gravity becomes strong that the two diverge. In those regions general relativity must be used.
A discussion of general relativity is outside the scope of what we can address here, and I bring it up only as an illustration. When we see motions of objects in space that we cannot explain given the amount of gravitating mass we see, there are two possible conclusions. The first is that there are unseen bodies present, creating extra gravity and perturbing the motions of objects. We can then look for those objects and try to reconcile the orbital motions with the gravitating mass. The other possibility is that our application of the gravitational equations is in error, and that we need a different theory of gravity. The latter turned out to be the explanation for Mercury, though for decades astronomers believed the solution was in the existence of unseen matter in the form of the planet Vulcan.
But sometimes things have gone the other way. The discovery of Neptune was greatly aided by the realization that Uranus moved in ways not explained by the gravity of the Sun - and the known planets - alone. Uranus’s orbital motions suggested that an unseen body tugged at it from a place farther out in the solar system. That body, the planet Neptune, was eventually found. It was this success of Newton’s gravitational theory in the 19th century that emboldened scientists to postulate the existence of Vulcan, and to spend so many years vainly looking for it. It is also the example of Neptune’s discovery that suggests the presence of unseen matter can sometimes be the explanation for puzzling motions of celestial objects.
Evidence for Dark Matter - I. Galaxy Clusters
In the 1930s, astronomers began to study the universe beyond our galaxy. It was only at the very end of the previous decade, in 1929, that Edwin Hubble had presented the evidence that the universe even extended that far. Prior to that, many astronomers had thought that the nebulae that were, in fact, external galaxies, were no more than clouds of gas within the confines of the Milky Way. Hubble proved that this idea was wrong.
An astronomer at The California Institute of Technology (Cal Tech) named Fritz Zwicky soon began to study a group of these external galaxies in the constellation Coma Bernices (Bernice’s Comb), called the Coma cluster. He measured the motions of the galaxies within the cluster and found them to be exceedingly fast. Zwicky then counted up the amount of matter he could see, basically the galaxies themselves, which allowed him to assign a total mass to the cluster. When he compared the galaxy speed to the mass he saw that there was far, far too little mass to hold the cluster together. Instead, given the speed of the galaxies and the paltry amount of mass, the Coma Cluster should be flying apart.
Of course, it is possible that the Coma cluster is, in fact, flying apart. But it seems unlikely. The universe, it turns out, is full of such galaxy clusters, and one has to wonder why we should see them at all if they are not stable. Zwicky understood this too, so he postulated the existence of additional mass that was invisible to him. Being German-Swiss originally, he coined a German term for this missing mass, “dunkel Materie,” or dark matter.
Zwicky’s method of mass determination was not the same as that described above. He used energy considerations, not forces and accelerations. Specifically, he used the Virial Theorem. Nonetheless, the methods are complementary, not at odds. Both should (and do) give the same results. It’s just that for some systems, forces and accelerations provide the simplest approach. For others, it is easier to use energy. In either case, we arrive at a mathematical relationship like the one above, with \(M \approx v^2 r / G\), with \(v\) being a characteristic speed for components in the system and \(r\) being a characteristic size.
Zwicky’s initial estimates of the amount of dark matter were far too large because he used an incorrect conversion of light, basically the brightness of galaxies, which he was able to measure, to mass, which he had to infer from the light he saw. This was in the early days of our understanding of galaxies, and subsequent research has brought the amount of mass associated with a given amount of light down considerably. Nonetheless, even with the current much lower conversions, the motions of individual galaxies within clusters (as well as the temperature of the x-ray emitting gas they contain) suggests that they have approximately six times as much matter as we see in them. This result holds true for all galaxy clusters, not just Coma. So the dark matter puzzle has not gone away. An image of the Coma cluster from the NASA website Astronomy Picture of the Day (APOD) is shown below.

Evidence for Dark Matter - II. Galaxy Rotation Curves
Clusters are not the only evidence for dark matter. In the 1970s, an astronomer named Vera Rubin began to study the rotation of spiral galaxies. What she found was unexpected. To understand why, let’s consider the rotation of the planets around the Sun. According to our analysis above, their velocity should decrease as the square root of their distance from the Sun. Up above, we learned that the velocity squared of an object orbiting another object is given by the following expression.
$$v^2 = \frac{GM}{r}$$
We can take the square root of both sides of this equation to arrive at the equation below. We have rewritten the square root of the product \(GM\) as a single constant, \(k\), to emphasize the dependence on the orbital radius, \(r\). To take one example, the equation predicts the orbital speed for all the planets.
To compare this prediction to observation, we can plot the observed planet orbital speeds with a plot of the equation on the same graph. The figure at right below shows such a comparison. You can see that the prediction matches the observations extremely well.
$$v = \frac{k}{\sqrt{r}}$$
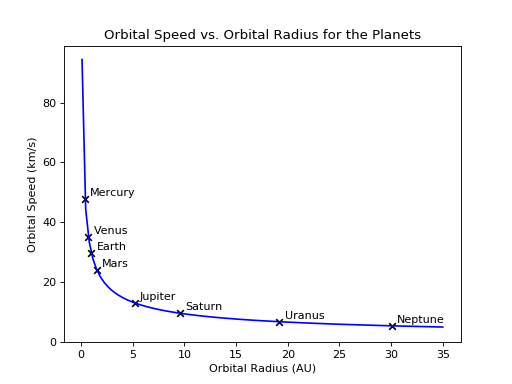
This \( r^{-\frac{1}{2}} \) dependence is what we expect for a system like the Sun and planets, in which nearly all the mass is located in the central object. But what about a galaxy?
The mass distribution of galaxies is very different from the mass distribution of planetary systems orbiting a star. Galaxies do seem to have a mass concentration near their center, but they also have considerable mass away from the center. As a result, we expect that the velocity of the stars in a galaxy will not fall off as rapidly as the velocity of the planets in the solar system does. However, it is not clear what sort of dependence to expect. It just depends how the mass in galaxies is distributed. Galaxy mass dependence with radius is what Very Rubin set out to explore when she began her study of spiral galaxies. To determine the mass distribution, she made careful measurements of stars in galaxies and plotted them against the distance of the stars from the galactic centers of the systems she observed. Example plots from one of her papers (Rubin et al, Astrophysical Journal, 289, 81, 1985) are shown at right.
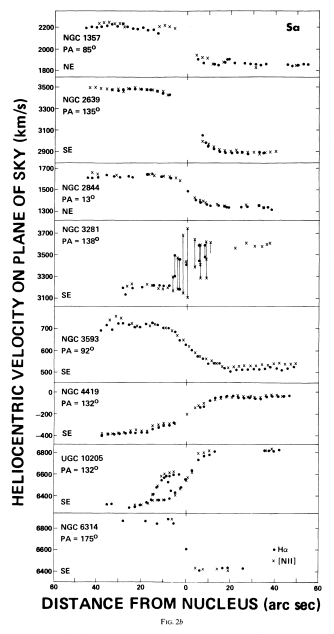
These graphs, which are called rotation curves, can be used to infer the radial dependence of gravitating mass in each of the galaxies plotted. Eight galaxies are shown here. The horizontal axis for the plots is angular distance from the galaxy center, in arc seconds. The vertical axis for each shows recession speed from Earth. Each is centered on the recession speed of the galaxy, which is typically several hundred or several thousand km/s. The half of the galaxy that is rotating away from us has a slightly higher recession speed, while the side of the galaxy that is rotating away from us has a slightly lower recession speed. We could subtract the system recession speed, which is the speed of the galaxy center, but that has not been done for these plots.
One difference that is immediately noticed from the plot of the solar system is the the velocities of stars in the outer parts of these galaxies is faster than rotation speeds for galaxies near the center. That is expected because as we move away from the center of a galaxy we are adding gravitating mass inside the orbits of the stars. However, what was surprising to astronomers was how the rotation curves all flatten out after some distance, and how they essentially remain constant out to the edge of measurements. Let’s look at the implications for the observed flattening of rotation curves.
From our discussion above, we know that the velocity of the stellar motion depends on the attracting mass and the size of the stellar orbits. We can rewrite the equation from above as below, but now we have expressly written the gravitating mass with a radial dependency, \(M = M(r)\). This reminds us that we no longer have a dominant massive object inside the orbit. Instead, the gravitating mass increases significantly as we move outward from the center, and so we expect that the rotation speed will increase, too.
Of course, the velocity does increase with radius in the inner parts of the galaxies. The plots clearly show this. However, at some radius, call it \(r_0\), the velocity becomes constant in all the galaxies, and each has its own particular value for the characteristic radius \(r_0\).
$$ v(r)^2 = \frac{GM(r)}{r}$$
If the velocity is remaining constant as the distance \(r\) increases, it must also be true that the mass \(M\) increases, and it must do so at exactly the same rate. So we must have an expression for the mass, at least in the region of the galaxies where the rotation speed is constant, that is like the one below. \(M_0\) and \(r_0\) are both constant parameters.
$$ M(r) = M_0 \left ( \frac{r}{r_0} \right )$$
With this sort of radial dependence for mass, the variable \(r\) cancels out of the equation, leaving a constant velocity.
$$ v^2 = \left (\frac{G}{r} \right ) \left [ M_0 \left ( \frac{r}{r_0} \right ) \right ] = \frac{GM_0}{r_0}$$
The need for dark matter becomes apparent when you take a look at a photograph of a spiral galaxy, like the one below. You will see that they are bright in the center and become progressively dimmer toward the edges. This is because the stellar density drops with radius.

One solution would be to make up the increasing mass with material that does not shine, like gas or dust. However, it turns out that gas and dust both shine quite brightly if you observe them in the right form of light. For example, we can observe the atomic gas via radio emission from neutral hydrogen, called HI. In areas that contain hydrogen molecules instead of atoms, emission from other molecular species (like CO) is visible. The dust, on the other hand, is visible by infrared emission. So we actually can observe these constituents, and none of them can explain the constant rotation speed of galaxies. What’s more, the emission from neutral hydrogen extends many times farther from the center than the stars, dust and molecular gas do. Even at these distances the rotation speed remains constant, indicating that the mass within the galaxy continues to increase with radius as far out as we can measure.
Only a small fraction of the mass is observed directly at these distances by electromagnetic radiation. Instead, the vast majority of the mass is completely invisible, and this invisible material dominates the total mass of the entire galaxy by as much as a factor of ten. Somewhat confusingly, the material composing the bulk of the mass is called dark matter. But it’s not really dark, it’s invisible. Invisible matter would be a much more descriptive and less confusing name for it.
Evidence for Dark Matter - III. Gravitaional Lensing

Abel 2218 galaxy cluster and gravitational lensing system.
Credit: NASA, ESA, and Johan Richard (Caltech, USA) Acknowledgement: Davide de Martin & James Long (ESA/Hubble)
The image above illustrates the third type of powerful evidence for dark matter: gravitational lensing. This phenomenon is not part of Newtonian physics, according to which, gravity would arguably not have any effect on light at all. Because light has no mass, it would not feel any force according to Newton’s Law of Universal Gravitation. I say arguably because there is another view of Newtonian gravity in which it is thought of an an acceleration (the little g, discussed above) and not a force, per se. In that case, everything could experience the acceleration, even light. However, if you compute the deflection caused by a Newtonian acceleration as light passes a massive object, you find that you predict only half the amount of deflection that is observed. This deflection was first measured during a solar eclipse in 1919, after it had been predicted by general relativity - Einstein, again. The predictions of GR match the deflection observed precisely.
As mentioned before, GR is too much to go into in this post. However, we will go so far as to say that in the GR view of gravity, it is neither a force nor an acceleration. It is a distortion of space and time (spacetime, in the parlance of relativity, both special and general). This distortion is a compression or stretching of space, and similarly, a slowing or speeding up of time, and the effects are local and vary as one moves around in spacetime. The distortion (which is gravity) causes the trajectories of objects to appear to bend. It also makes it seem as if there is a gravitational acceleration near massive objects. But there is no acceleration in 4-dimensional (3-space plus 1-time dimension) spacetime. The apparent acceleration is an illusion that appears in 3-dimensional space when you consider it separate from time, as is the case with Newtonian physics. Even if you ddin’t follow all of that, you probably get that it is a completely different view of what gravity is and how it works. What’s more, it does a better job than Newtonian gravity of predicting how gravity behaves and how it affects objects in the universe. All objects.
Just as Newtonian dynamics can be used to infer the gravitating mass in a dynamical system, so general relativity can be used to infer the mass in a system with gravitational lensing, which is itself a dynamical system, of course. When this is done, we again find that the amount of mass required to cause the observed bending of starlight is much greater than the mass that can be directly observed in light, radio, x-rays, infrared, etc. So again, we have strong evidence for invisible material affecting the gravitational field, or in other words, for dark matter.
The picture above is a Hubble Space Telescope image of the galaxy cluster called Abel 2218. If you look closely you will notice many arc structures that are concentric around the cluster center. You can also see arcs centered around some of the more massive cluster members. These arcs are actually images of background galaxies that have been distorted by the gravity (spacetime distortion) of the foreground cluster mass. Astronomers call such a system a gravitational lens because the mass of the cluster acts like a lens to magnify and distort objects in the background. A system like this, with very prominent and obvious arcs, is called a strong lens, and it provides powerful means to determine the mass in the cluster. Analysis of the arcs provides a way to measure not just the total mass in the lens, but also the mass distribution required to form the many images seen. So gravitational lensing alone suggests the existence of dark matter, because the amount of mass required to create the lensed images is always much more than is observed via electromagnetic waves. Furthermore, the mass determined by lensing agrees with the mass determined for clusters using more traditional methods based on the velocities of the cluster members, as Zwicky first used back in the 1930s.

Bullet Cluster. For more information about this image:
http://chandra.harvard.edu/press/06_releases/press_082106.html
The second image provides the most powerful evidence for dark matter yet seen. It shows a collision between two galaxy clusters, but there is a lot going on here and it needs a bit of explaining. There are actually three images superimposed. The first is the optical image of the galaxies, and it does not show anything particularly unusual. There is not even any strong lensing as observed for Abel 2218. However, careful analysis of galaxies in this field shows that they are slightly distorted by the mass of the clusters. The distortion is not enough to be seen in any individual galaxy, but when considered as a whole, the galaxies tend to be curved into arcs centered on the mass in the foreground, just as is the case for the individual galaxy arcs in the strong lens of Abel 2218. Analysis of this weak lensing effect shows that the mass of the clusters is concentrated in the areas shaded blue. Note that these areas coincide with the two clusters in the image. Not a big deal, you might think, but just wait.
Finally, there is the red region. This is x-ray emission that has been measured by the Chandra X-Ray Observatory, a counterpart to Hubble that observes the universe in the higher energy regime of x-rays. This Chandra image shows the presence of very hot gas, with a temperature of several million kelvin.
Putting this all together, we have the following picture: Two clusters collided with each other quite recently (cosmically speaking). The member galaxies of each cluster pretty much passed right through one another. That would be expected since the clusters are mostly empty space, and the distance between galaxies in each cluster is much larger than the galaxies themselves. You can think of if sort of like two swarms of bees that pass through one another. The bees will seldom, if ever, run into one another, and the swarms will continue along on their journeys unmolested. A similar condition exists when two galaxies collide because the distance between stars in a galaxy is much larger than the stars themselves, to an even greater degree, in fact.
But look at the distribution of the x-ray emitting gas. It has stopped in the middle of the two galaxy clusters, presumably the point of the collision.
All galaxy clusters contain this hot gas. In fact, there is as much mass in cluster gas as there is in the stars in the member galaxies. However, if two clouds of gas collide, they do not pass through one another. The gas particles (atoms, in this case) interact very strongly via collisions, or in other words, through strong electromagnetic interactions. All of their kinetic energy (energy of motion) has gone into heating them up, while they themselves have pretty much stopped dead in their tracks. This is what we see has happened from the Chandra image.
So the collision has stripped the gas out of the two clusters, but the galaxies and the bulk of the mass (revealed by weak lensing) has passed through. This indicates that the material that strongly interacts via electromagnetic effects - the gas component of the mass that can collide - has stopped. The components that do not interact via electromagnetic effects, the galaxies and whatever is causing the lensing, have passed right through and continued on their original trajectories. This is exactly what would be expected for a dark matter particle that has mass, and so interacts via gravity, but that has no ability to respond via electric or magnetic interactions.
Most astronomers consider this system, and a couple others like it, to be the final proof needed for the existence of dark matter, an invisible type of particle that interacts only, or at least primarily, by gravitational effects. Dark matter is invisible because, lacking any electromagnetic potency, it does not interact with any electromagnetic radiation, not visible light, not x-rays or gamma-rays, not ultraviolet, not infrared, not radio. Nothing. But it has mass/energy, and according to general relativity, anything that has mass or energy will both create gravity (spacetime distortion) and respond to it.
What is the Dark Matter?
The discussion above gives a general overview of the reasoning behind the belief among most astronomers and physicists that the vast majority of the matter in the universe is invisible. When scientists do a census, the dark component of matter is more than 85% of the total. And by “invisible,” we mean a type of matter that does not interact via electromagnetism. It is not detectable using light (photons) of any kind. Such matter is clearly not composed of the standard kinds of particles, leptons (basically electrons) and baryons (particles made of quarks, like protons and neutrons), since they both interact strongly with photons. Well, almost.
One type of lepton, the neutrinos, do not interact with electromagnetic radiation. Could they be the dark matter? For a time, many physicists and astronomers thought they might be. However, when the details of neutrino dark matter are worked out, they turn out to have the wrong properties. Indeed, they are dark, but the dark matter in galaxies and galaxy clusters is far too concentrated to be predominantly neutrinos. Because of their tiny mass, which is almost zero, in fact, they are moving very fast. And because they interact so weakly, they cannot cool down (and thus slow down). Cooling down means that a substance transfers its kinetic energy to some other object or substance, and material that does not interact with anything cannot do that. Of course, neutrinos do interact via gravity, but gravity is too weak to account for much cooling for a fast-moving particle. For this reason, there is no way for neutrinos to collapse into the concentrated structures that we observe in galaxies and galaxy clusters. Neutrinos are a type of dark matter, but they can only be a tiny fraction of what is seen dominating galaxies and clusters. That dark matter must be something else.
So what could it be? In truth, we don’t know. We know from its distribution in space (collapsed into concentrated lumps) that it must be “cold.” That means it must be a particle that is fairly massive, so that even at high temperatures it would move slowly. Only in that way could it have managed to cool via gravitational interactions, the only kind available to it, and collapse when the universe was young. It could have thereby seeded the collapsed structures we see today.
There are no particles in the zoo of known particles that have the right properties to account for such an early collapse. The dark matter must be some kind of as yet unknown particle. Scientists have proposed a number of candidates, but to date, none of them has been detected. Thus far the dark matter is only detected indirectly via the motions of the stars and galaxies, and in the bending of light in gravitational lenses.
